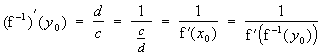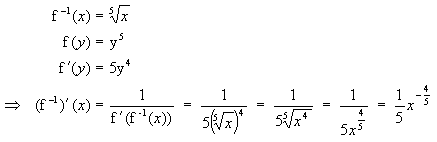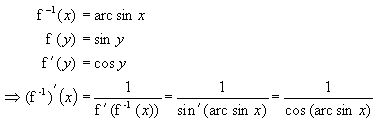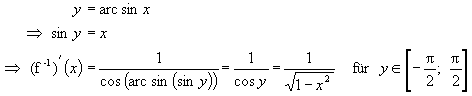Umkehrfunktionen und ihre Ableitung
Als Umkehrfunktion einer Funktion f (rot) wird diejenige Funktion bezeichnet,
die sich ergibt, wenn man f an der Spiegelachse x=y (schwarz) spiegelt.
Diese bezeichnet man als f-1 (in den Zeichnungen violett). Aus
computertechnischen Gründen konnten wir sie in unseren Zeichnungen
leider nur mit f* bezeichnen. Also: f*=f-1 .
Rechnerisch erhält man f-1, indem man die Gleichung
f(x)=y zunächst nach x auflöst und danach die Variablen vertauscht.
| Beispiel: |
1.) |
f(x) |
= |
x3 - 2 |
|
|
=> y |
= |
x3 - 2 |
|
|
=> x |
= |
(y+2)1/3 |
|
2.) |
y |
= |
(x+2)1/3 |
|
|
=> f-1(x) |
= |
(x+2)1/3 |
Zur Verdeutlichung hier nun ein Bild der Funktion f(x) = 2 ln x
und der dazugehörigen Umkehrfunktion:
|
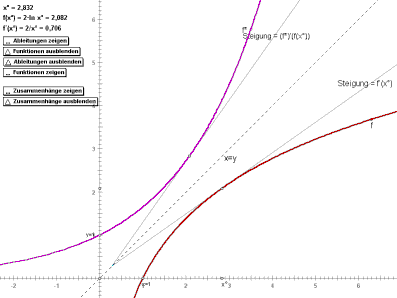
Wenn man x0
hin- und herbewegt, sieht man, wie sich die damit zusammenhängenden
Werte bei f und f-1 sowie deren Tangenten verändern.Außerdem
erkennt man deutlich, daß die zu den Funktionen gehörigen Ableitungen
in keinerlei ähnlichen Zusammenhang stehen.
Läßt man sich jedoch die Zusammenhänge
anzeigen,sieht man, daß die Tangentensteigung von f-1(y0)
der Kehrwert der Tangentensteigung von f(x0)
ist.
|
Dieses Bild zeigt den selben Zusammenhang in einer Zeichnung,
die mit The
Geometer's Sketchpad erstellt wurde. Um die Zeichnung zu sehen, muß
eine Sketchpad-Version (erhältlich für Macintosh oder Windows,
auch als Demo)
auf eurem Rechner installiert sein. Außerdem muß euer Browser
so eingestellt sein, daß er Dateien mit der Endung .gsp mit Sketchpad
öffnet. Dann könnt ihr die Zeichnung mit einem Klick auf das
Bild laden.
|
Die Ableitung der Umkehrfunktion
In dem Bild soll die blaue Seite des Steigungsdreiecks von f(x0)
d und die gelbe Seite c heißen. Dies bedeutet, daß f '(x0)
= c/d.
Dies wiederum heißt, daß gilt:
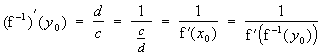
Nach Vertauschen der Variablen ergibt sich die Umkehrregel in der üblichen
Gestalt:
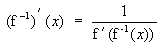
In Fällen, in denen die Ableitung und die Umkehrfunktion einer
Funktion bekannt sind,
läßt sich auf diese Art und Weise die Ableitung der Umkehrfunktion
berechnen.
Beispiel:
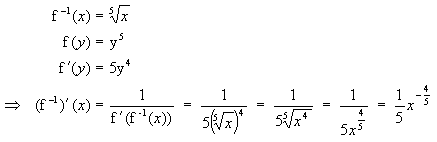
Weil dieses Ergebnis sich auch mit Hilfe der Potenzregel für den
Exponenten 1/5 ergibt, hilft uns die Umkehrregel, die Potenzregel auf gebrochene
Exponenten fortzusetzen. (Zu Beginn wird die Potenzregel nur für natürliche
Exponenten bewiesen.)
Zur weiteren Verdeutlichung wollen wir nun noch ein letztes Beispiel
bringen:
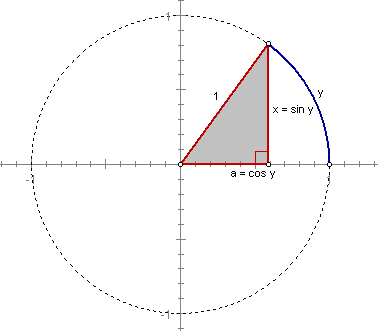
Auf dem Intervall [-1, 1] ist arcsin die Umkehrfunktion von sin, es
gilt für alle x aus dem Intervall ]-1,1[ :
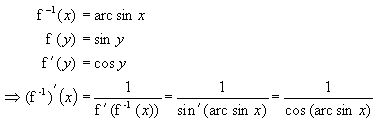
Sei
Damit soll dieses Kapitel beendet sein.