Geometrical Paradox
Bamboozlement is a term suggested by
Greg Frederickson to describe plane dissections, followed by rearrangment
of pieces that result in a figure of supposedly different area.
Curry's Paradox
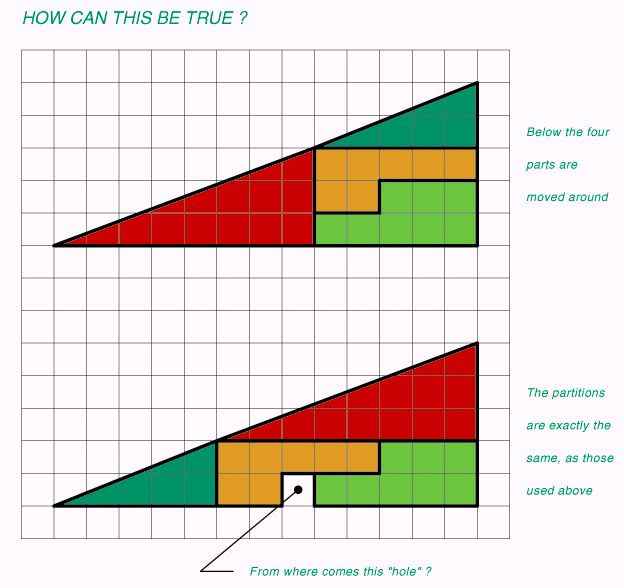 This is Martin Gardner's modified version of Curry's paradox.
An extensive history and explanations are given in [Martin Gardner, 1956].
See also [Frederickson, 1997]. The picture made Daniel Takacs.
This is Martin Gardner's modified version of Curry's paradox.
An extensive history and explanations are given in [Martin Gardner, 1956].
See also [Frederickson, 1997]. The picture made Daniel Takacs.
A Chessboard Paradox
Sam Loyd presented this fallacy one the first American Chess congress 1858.
The first time this was seen in print was (1868), a "Kurze Mitteilung" of
the Editor O. Schlömilch. Eleven years later (1879) Schlegel published the
Fibonacci generalization.
 Alex Bogomolny made an applet
Fibonacci Bamboozlement
where you can shift the pieces for squares of Fibonacci number size.
Alex Bogomolny made an applet
Fibonacci Bamboozlement
where you can shift the pieces for squares of Fibonacci number size.
Rectangular Transformation Paradox (4 Pieces)
Given three numbers x0, x1, x2
in almost geometric progression which means that
x1 x1 - x2 x0 = µ is small.
The following figure shows half of a
x1 by x2 + x1 rectangle.
+ ,
| ' ,
| ' ,
| ' ,
| | ' ,
x1 | ' ,
| | ' ,
| x0 ' ,
| | ' ,
| | ' ,
+------ x2-x0 -------+---------- x1+x0 ---------------------+
Rearranging the four pieces gives a
x0 + x1 by x2 rectangle.
The area difference between the first and the second
rectangle is µ.
The classical parameters given by Sam Loyd are
(x0, x1, x2, µ) = (3, 5, 8, 1),
three consecutive Fibonacci numbers, in which case one rectangle is a square as
x0 + x1 = x2.
Other transformations are given in the table below.
x0 x1 x2 µ x1 × x1+x2 x0+x1 × x2 area1 area2 reference
4 5 6 1 5 × 11 9 × 6 55 54 [Walter Lietzmann]
3 5 8 1 5 × 13 8 × 8 65 64 [Sam Loyd]
5 6 7 1 6 × 13 11 × 7 78 77
4 7 12 1 7 × 19 11 × 12 133 132
5 8 13 -1 8 × 21 13 × 13 168 169
2 7 24 1 7 × 31 9 × 24 217 216 [Hermann Schubert]
4 9 16 1 9 × 25 14 × 16 225 224
5 11 24 1 11 × 35 16 × 24 385 384 [Torsten Sillke]
|
Typically you find the note that this transformation can be made for arbitrary
rectangles A*D and B*C if |A*D - B*C| = 1. But this is not true.
[Lietzmann 1972] and [Devendran 1985]
correctly say that we must have A+B=D in addition.
I think my parametrization is more suitable for this dissection.
Rectangular Transformation Paradox (6 Pieces)
Given three numbers x0, x1, x2
in almost geometric progression which means that
x1 x1 - x2 x0 = µ is small.
The following figure shows half of a
x1 by x2 + 2x1 rectangle.
+ ,
| ' ,
| | ,
| | ' ,
| | ' ,
x1 | ' ,
| | ' ,
| 2*x0 | ' ,
| | | ' ,
| | x0 ' ,
| | | ' ,
+--- x2-4*x0 ---+------------- x1+2*x0 -------------+------------- x1+2*x0 -------------+
Rearranging the six pieces gives a
2x0 + x1 by x2 rectangle.
The area difference between the first and the second
rectangle is 2µ.
x0 x1 x2 µ x1 × 2x1+x2 2x0+x1 × x2 area1 area2 reference
2 5 12 1 5 × 22 9 × 12 110 108 [Torsten Sillke]
3 8 21 1 8 × 37 14 × 21 296 294 [Torsten Sillke]
|
This construction can be generalized. So we have an 8 piece transformation of a
x1 by x2 + 3x1 rectangle into a
3x0 + x1 by x2 rectangle where
the difference of their areas is 3µ.
Cassini's Fibonacci identity
Many Bamboozlements use Fibonacci numbers.
One of the oldest theorems about Fibonacci numbers, due to the French astronomer
Jean-Dominique Cassini
in 1680, is the identity
Fn+1 × Fn-1 - Fn × Fn = (-1)n.
The shortest proof of this identity is via the matrix identity which is another way of
writing the recurrence formular. Then use the theorem that the determinant is
multiplicative.
n
[ 1 1 ] [ Fn+1 Fn ] n | Fn+1 Fn |
[ 1 0 ] = [ Fn Fn-1 ] => (-1) = | Fn Fn-1 |
There is a geometric reasoning if we compare the two rectangles
Fn+1 × Fn-1 and
Fn × Fn. They both contain the rectangle
Fn × Fn-1. This means
Fn+1 × Fn-1 =
Fn × Fn-1 +
Fn-1 × Fn-1 and
Fn × Fn =
Fn × Fn-1 +
Fn × Fn-2. Their difference is
Fn+1 × Fn-1 - Fn × Fn =
- (Fn × Fn-2 - Fn-1 × Fn-1).
Showing the relation for n=1 with F2 = F1 = 1 and F0 = 0
completes the proof.
A combinatorial interpretation of the relation of Cassini was published by
N. Werman and D. Zeilberger.
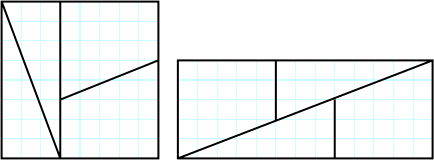
Supplement Rectangles for Curry's Paradox
For a Curry triangle we can make a two piece zig-zag dissection of
the supplement rectangle if the width of the rectangles differ by one.
A first sequence of pairs of rectangles is
x x x x x x x x x x x x x x x
+ x + + x x x + + + x x x x x
+ x + + + x x + + + + + x x x
+ + + + + + + + + + + + + + +
+ x x + + x x x x x + + + x x x x x x x x
+ . x + + + . x x x + + + + + . x x x x x
+ + x + + + + + x x + + + + + + + + x x x
A second sequence of pairs of rectangles is
x x x x x x x x x x x x x x x
x + x x x x + + x x x x x x x
. + + . x x + + + + . x x x x
+ + + + + x + + + + + + + x x
+ + + + + + + + + + + + + + +
x + x x x x x + + x x x x x x x x x
x + + x x x x + + + + x x x x x x x
+ + + + + x x + + + + + + + x x x x
+ + + + + + x + + + + + + + + + x x
The hole need not be in the middle but this looks nicer.
Euclid's Supplement Parallelograms
A parallelogram is dissected by a diagonal into to congruent triangles.
C-----------F-------------------I
/ / , /
/ / , /
/ / , /
/ / , /
B-----------E-------------------H
/ , / /
/ , / /
A-----------D-------------------G
Select a point E on the diagonal. Draw lines through E which are
parallel to the sides of the parallelogram. As a result we get
four small parallelograms. Now Euclid says: The two supplement
parallelograms DGHE and BEFC have the same area.
If E is not on the diagonal then we have two quadrangles AGIE
and ACIE. And area(AGIE) - area(ACIE) = area(DGHE) - area(BEFC)
but this is not null. This explains the paradoxes. The 'traingles'
are quadrangles.
Area of a Parallelogram
What is the area of a parallelogram generated by two vectors
X=(a,b) and Y=(c,d)? The corners of the parallelogram are
0, X, Y, and X+Y. Now assume that a, b, c, and d are positive.
Our 'paradox' shows that the area is
|a*d - b*c| the determinant of the vectors X and Y.
The angle t between X and Y is t = arctan(b/a) - arctan(d/c).
Using the scalar product we get the equations
|X|*|Y|*sin(t) = Area and
|X|*|Y|*cos(t) = X*Y. Division gives
tan(t) = Area/(X*Y).
Substitute the parameter of the chess board dissection gives
X=(8,3), Y=(5,2). Then the area=1 and X*Y=46.
So t = arctan(1/46) which is nearly 1/46.
This follows from the alternating series
arctan(x) = x - x3/3 + x5/5 - ... .
Converting Rad to Degree gives 1.245 which is rather small.
References
-
W. W. Rouse Ball, H. S. M. Coxeter;
Mathematical Recreations & Essays,
Cambridge 1974, 12th edition
(1st ed., 1892, pp. 34-36. 8 x 8 to 5 x 13 and generalizations)
Chapter 3.2 Geometrical Paradoxes, 3rd Paradox
- 4 piece dissection showing 8*8 = 5*13 and Fibonacci generalization;
(continued fraction convergents)
-
Karl Ferdinand Braun;
Der junge Mathematiker und Naturforscher:
Einführung in die Geheimnisse der Zahl und Wunder der Rechenkunst,
Otto Spamer Verlag, Leipzig 1876
(Reprint: Geheimnisse der Zahl und Wunder der Rechenkunst,
Rowohlt Verlag, Reinbeck 2000, ISBN 3-499-60808-1, p72-76)
Chapter 3
-
M. Busch;
Über einen geometrischen Trugschluß,
Mathematisch-Naturwissenschaftliche Blätter 13 (1916) 89.
-
Stuart Dodgson Collingwood;
The Lewis Carroll Picture Book,
T. Fisher Unwin, 1899.
(Reprint: Dover, 1961, with new title:
Diversions and Digressions of Lewis Carroll)
-
T. Devendran (editor);
Neues aus dem Mathematischen Kabinett,
Hugendubel Verlag, München 1985
Section II.2: Fibonacci und die Bienen (Thomas Hartkopf, Siegfried Rösch)
(continued fraction convergents A/B and C/D with the constraint A+B=D)
Shows Schubert's 7/24 to 9/31 example.
-
Henry E. Dudeney;
Amusements in Mathematics, Thomas Nelson and Sons, London 1917, p141, 247
(Reprint: Dover, 1958, ISBN 0-486-20473-1)
problem 413: A Chessboard Fallacy
- 3 piece dissection showing n*n = (n+1)*(n-1)
-
John Fisher;
The Magic of Lewis Carroll,
Thomas Nelson and Sons, 1973
(german: Alice im Wunderland der Rätsel,
Hugendubel, 1985, ISBN 3-88034-268-7, p66-67)
- 4 piece dissection showing 8*8 = 5*13
-
Greg. N. Frederickson;
Dissections: Plane & Fancy,
Cambridge Univ. Press, 1997
- chapter 23
-
Greg. N. Frederickson;
Geometric dissections on the web
-
David Gale;
Tracking the Automatic Ant,
Springer Verlag, 1998
Chaper 16.Addendum: Jigsaw Paradoxes, 128-130.
(Reprint of: Mathematical Intelligenzer 17:1 (1995) 25-26 and
the correction 17:2 (1995) 39)
- Jean Brette's multiple reorderings of a right 9x16 triangle
-
Martin Gardner;
Mathematics, Magic and Mystery, New York, Dover Publ. 1956
(german: Mathematik und Magie, DuMont, 1981 Tb 106, ISBN 3-7701-1048-X and
Mathemagische Tricks, Vieweg 1981)
Capter 8: Geometrical Vanishing Parts II,
Best extensive discussion of the subject and its history.
- Paradox of William Hooper (1794)
- Paradox of Langman (variation of William Hooper)
- Paradox of Paul Curry (1953)
- Zig Zag Dissection of an 'Rectangle' into two pieces
-
Martin Gardner (Ed.);
Best Mathematical Puzzles of Sam Loyd, New York, Dover Publ., 1959
(german: Sam Loyd, Martin Gardner; Mathematische Rätsel und Spiele, Dumont, 1978)
problem 24: The Gold Brick problem
- 3 piece dissection showing n*n = (n+1)*(n-1)
-
Martin Gardner;
The Scientific American Book of Mathematical Puzzles and Diversions,
Simon & Schuster (1959)
Chapter 14: Fallacies (the Curry triangle)
-
Martin Gardner;
The Second Scientific American Book of Mathematical Puzzles and Diversions,
Simon & Schuster (1961)
Chapter 8: Phi: The Golden Ratio
- 4 piece dissection showing (a+b)*(a+b) = b*(a+2b). See Fig. 44
-
Martin Gardner;
New Mathematical Diversions from Scientific American,
Simon & Schuster (1966)
Chapter 11: Mr. Apollinax Visits New York
- Figure 50 is a missing hole configuration (also shown in [Gardner 1998])
-
Martin Gardner;
aha! Gotcha Paradoxes to puzzle and delight,
Freeman, 1982, New York-San Francisco
(german: Gotcha, Pradoxien für den Homo Ludens, Hugendubel 1985)
- Randi's carpet, p72-74
-
Martin Gardner;
A Quarter-Century of Recreational Mathematics,
Scientific American. (Aug 1998) v. 279(2) p. 68-75
Zbl 1999f.04107
(Ein Vierteljahrhundert Unterhaltungsmathematik,
Spektrum der Wissenschaft, (Nov 1998), 112-120)
- Das Paradox vom verschwundenen Loch, p117, 120 [Gardner 1966]
-
Ron L. Graham, Donald E. Knuth, Oren Pataschnik;
Concrete Mathematics,
Addison Wessley, Reading, 1994, 2nd Ed.
Chapter 6.6 Fibonacci Numbers, Excercise 6.75
- 4 piece dissection showing 8*8 = 5*13
-
Hjärnbruk;
swedish page www.fof.se/main/hjarnbruk/
showing some dissections found in Martin Gardner MM&M [1956].
- Trollar bort rutor
- Currys triangle
- Schackkongressen 1858
- Lösningarna
-
William Hooper;
Rational Recreations. 1774. Vol. 4,
pp. 286-287: Recreation CVI _ The geometric money.
3 x 10 cut into four pieces which make a 2 x 6 and a 4 x 5.
(The diagram is shown in Gardner, MM&M [1956], pp. 131-132.)
-
E. I. Ignatjew;
Mathematische Spielereien, 1982, 2nd Ed. ISBN 3-87144-646-7
first russion edition is from 1908.
Chap 8: Geometrische Sophismen und Paradoxa
- 4 piece dissection showing 8*8 = 5*13
-
Johnson;
Fibonacci Quarterly 41 (2003) B-960, pg 182.
F(a)F(b) - F(c)F(d) = (-1)r( F(a - r)F(b - r) - F(c - r)F(d - r) )
5F(a)F(b) - L(c)L(d) = (-1)r( 5F(a - r)F(b - r) - L(c - r)L(d - r) )
with a+b=c+d for any integers a,b,c,d,r
-
Ron Knott;
Harder Fibonacci Puzzles
shows
- A Fibonacci Jigsaw puzzle or How to Prove 64=65
- The same puzzle but losing a square or How to Prove 64=63!!
- Yet another Fibonacci Jigsaw Puzzle!
-
Boris A. Kordemsky;
The Moscow Puzzles,
1972,
problem 357: a paradox
(german: Köpfchen muss man haben, 1975, problem 320)
- 4 piece dissection showing 8*8 = 5*13
-
W. Lietzmann, V. Trier;
Wo steckt der Fehler? Trugschlüsse und Schülerfehler,
B. G. Teubner, Leipzig, 1913, p17
Series: Mathematische Bibliothek Band 10
Trugschluss 22: 63 = 64 = 65
- 4 piece dissection showing 8*8 = 5*13
-
Walter Lietzmann;
Wo steckt der Fehler?
B. G. Teubner, Stuttgart, 1972, 6. Auflage, p92-93,
ISBN 3-519-02603-1
Trugschluss V.9: 64 = 65
- 4 piece dissection showing 8*8 = 5*13
- general case b*c and a*d rectangles with the
constraints d=a+b and |b*c-a*d| = 1.
-
Sam Loyd;
The 8th Book of Tan, New York, Loyd & Co. Publ. 1903
(reprint: New York, Dover Publ, 1968)
- Tangram paradoxes
-
Sam Loyd;
Cyclopedia of Puzzles,
Franklin Bigelow Corporation, Morningside Press, New York, 1914
pages 288 and 378: Puzzleland Chess Boards
- 4 piece dissection showing 63 = 8*8 = 5*13
- He writes that he invented this dissection and presented it
one the first American Chess congress 1858.
page 32: The Gold Brick Problem
- 3 piece dissection showing n*n = (n+1)*(n-1)
-
M. Edouard Lucas;
Récréations Mathématiques II,
Gauthier-Villars, Paris, 1883
Section: Un Paradoxe Géométrique, p152-154
- 8*8 = 5*13 dissection and Fibonacci generalization;
-
mathworld.wolfram.com
- Triangle Dissection Paradox
- Dissection Fallacy
- Curry Triangle
- Tangram Paradox
-
Mittenzwey;
Mathematische Kurzweil, Leipzig und Wien, 1880
Problem 299: - 4 piece dissection showing 8*8 = 5*13
-
William R. Ransom;
One Hundred Mathematical Curiosities,
Weston Walch, Publisher, Portland, Maine, 1955
Section: Gaining or Losing a Unit of Area, p29-33
- 4 piece dissection showing 63 = 8*8 = 5*13
- Fibonacci generalization, golden section
-
Gianni A. Sarcone;
Paradoxical Tangram and Vanishing Puzzles,
Journal of Recreational Puzzles 29:2 (1998) 132-133
Problem 2424
-
Gianni A. Sarcone;
Paradoxical Tangram, Cubism For Fun 49 (June 1999) 17
- Tangram paradoxes (part of [Sarcone 1998])
-
V. Schlegel;
Verallgemeinerung eines geometrischen Paradoxons.
Zeitschrift für Mathematik und Physik 24 (1879) 123-128 & Plate I.
- 8 x 8 to 5 x 13 and generalizations.
-
O. Schlömilch;
Ein geometrisches Paradoxon,
Zeitschrift für Mathematik und Physik 13 (1868) 162
- 4 piece dissection showing 8*8 = 5*13
-
Hermann Schubert;
Mathematische Mußestunden, (kleine Ausgabe)
G. J. Göschen'sche Verlagshandlung, Leipzig 1904, 2. Auflage, p141-144
(Walter de Gruyter, Berlin 1941, 7. Auflage, p111-114)
- Chapter: Trugschlüsse,
8*8 = 5*13 dissection and Fibonacci generalization;
shows an 9*24 = 7*31 example; (continued fraction convergents)
-
David Singmaster;
Sources in Recreational Mathematics,
An Annotated Bibliography, 7th Pre. Ed., Oct. 1999
- Part II,
Sect. 6.P Geometric Vanishing
Sect. 6.P.1 paradoxical dissections of the chessboard
based on Fibonacci numbers
-
Jerry (= G. K.) Slocum, Jack Botermans;
Puzzles Old & New _ How to Make and Solve Them,
Univ. of Washington Press, Seattle, 1986
(german: Geduldspiele der Welt, Hugendubel, 1987)
- p144: vanishing puzzles
- 4 piece dissection showing 8*8 = 5*13 = 63 made from wood ca. 1900
-
Warren Weaver;
Lewis Carroll and a geometrical paradox,
American Mathematical Monthly 45 (1938) 234-236
- Describes unpublished work in which Carroll obtained (in some way)
the generalizations of the 8 x 8 to 5 x 13 in about 1890-1893.
-
N. Werman, D. Zeilberger;
A bijective proof of Cassini's Fibonacci identity,
Discrete Mathematics 58:1 (1986) 109
Zbl. 578.05004
Cassini's Fibonacci identity is
Fn+1 × Fn-1 - Fn × Fn = (-1)n.
-
William F. White;
A Scrap-Book of Elementary Mathematics. Open Court, 1908.
[The 4th ed., 1942, is identical in content and pagination,
omitting only the Frontispiece and the publisher's catalogue.]
- Geometric puzzles, pp. 109-117
8*8 = 5*13 = 63
-
Alex Bogomolny;
A Faulty Dissection: What Is Wrong?
and its solution
Fibonacci Bamboozlement
- an applet showing an 4 piece dissection using the relation
Fn × Fn - Fn-1 × Fn+1 = (-1)n+1
where Fn is the n-th Fibonacci number.
-
Alex Bogomolny;
Curry's Paradox: How Is It Possible?
- an applet for Curry's Paradox, Cassini's Fibonacci identity.
-
Alex Bogomolny;
Eye Opener Series
- an applet showing an 2 piece dissection using the relation
n × n versus (n+1) × (n-1).
-
Alex Bogomolny;
Technologies: Past and Future
- The WWW didn't help to solve a 'Geometric Fallacy'
-
Markus Götz;
Rätsel
- 0021: Flächentreue Abbildung?
explains Curry's Paradox
-
Norbert Treitz;
Pflastersteine
- Fibonacci Bamboozlement shown at the MNU meeting
Hardware
-
Geometrex from Rex Games, Inc
GEOMETREX. Incredible Puzzles create a simple way to learn the
natural sequences of numbers, as well as, the Fibonacci and Lucas sequences.
The sequences of natural numbers and related sequences have astonishing
properties, which can be used in architecture or for creating paradoxical
puzzles.
-
TangraMagic from Tessellations
This is the tangram paradox of [Gianni A. Sarcone].
-
Quadrix from
Archimedes' Lab puzzles
(follow the link Math curiosities->The golden number.)
Torsten Sillke
Home |
FSP Mathematisierung |
Fakultät für Mathematik |
Universität Bielefeld
Last Update: 2004-10-13


