Tiling and Packing results of Torsten Sillke
Polycubes Problems
Pentacubes
Ekkehard Künzell wrote a book (in German) on games played with pentacubes.
There he explains his pentacube numbering system.
The book is sold by Ingo Uhl GmbH in Germany.
Look after the reservat book.
There is another human-friendly
pentacube naming system
from Kate Jones of Kadon Enterprises, Inc..
She made also a
hexomino naming system.
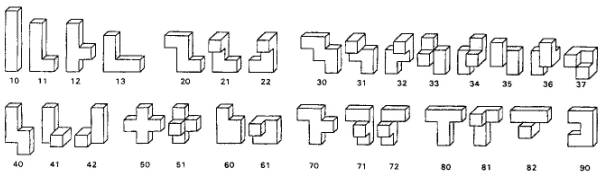
Here is my new systematic numbering scheme for polycubes.
It is the lexicographic numbering of the coordinates. Mirror images a noted by negative numbers.
Packing Boxes with like Pentacubes
- 10 - I-Pentomino (only the pentacube itself)
- 11 - L-Pentomino List complete
- 12 - Y-Pentomino List complete
- 13 - V-Pentomino List complete (3D)
- 20 - Z-Pentomino (found by Wolf in 1997)
- 21 - 21-Pentacube List incomplete
- 30 - W-Pentomino List incomplete
- 31 - 31-Pentacube List complete
- 33 - 33-Pentacube (5x8x8 by H. Postl)
- 35 - 35-Pentacube List (not boxable)
- 37 - 37-Pentacube (7x8x20 by H. Postl)
- 40 - N-Pentomino List complete (3D) by H. Postl
- 41 - 41-Pentacube List complete
- 50 - X-Pentomino (not boxable)
- 51 - 51-Pentacube (7x8x20 by H. Postl)
- 60 - P-Pentomino List complete
- 61 - 61-Pentacube List complete
- 70 - F-Pentomino List complete (3D)
- 71 - 71-Pentacube List complete
- 80 - T-Pentomino List incomplete
- 81 - 81-Pentacube List complete (3D)
- 82 - 82-Pentacube List incomplete
- 90 - U-Pentomino List complete
Box packings of Pseudo-Pentacubes. These need only be edge-conected.
Further one can consider not connected polycubes.
- Q5 - Pseudo-Pentomino List complete (3D) by H. Postl
- J5 - Pseudo-Pentomino List incomplete
- glider - Pseudo-Pentomino List complete (2+3D) by H. Postl
- large-u - Pseudo-Pentomino List incomplete
- o o . o . o o - tiling of the plane
Packings of handed Pentominoes. These problems have only been solved recently.
Packing Cubes
Cubes packed with identical pieces.
Cubes packed with mainly different pieces.
Packing Boxes with like Tetracubes
Packing Boxes with like Hexacubes
- G6 - G-Hexomino List incomplete
- p6 - p-Hexomino List complete
- Cube 6 - Cubes with like Hexacubes.
Packing Boxes with like Heptacubes
The following P-Heptacubes a simple box packers.
But the rectangles are hard. See Mike Reid.
- p7 - p-Heptomino List complete
- p7.2 - p2-Heptomino List complete (3D)
- p7.3 - p3-Heptomino List complete (3D) (the nost interesting one)
Other Polycubes Problems
Packing Polyspheres
Tilings with Matching Conditions
The Who is Who in Tiling and Packing
Tiling Programs
Tiling and Packing Links
Playing with Tetracubes
- Tetracubes
- Problems for Tetracubes without the blocks
(Update)
Playing with Pentacubes
Proofs and Techniques
You can find impossebility proofs in most of the box lists of like polycubes.
Most of these proofs are by bounds or modular (e.g. parity) restrictions.
Typical proofs are REHM's cubes and the
SOMA cube secrets.
Sometimes you analyse possible local configurations. The best example of
this type is Yuri Aksyonov's proof Handed Y5 rectangles.
These type of proof are considered simple proofs. I don't say they are simple to find.
I am especially proud of finding the 3-Bone Impossibles.
Sometimes you can show that counting is not enough to show impossibility.
For 2-dimensional problems you can than try to use the word-group method.
It had been used the first time by John H. Conway. You need some group
theory to see that such a proof does indeed proofs anything. And you
must be familiar with it (of a program like GAP) to find such proofs
of yourself. Mike Reid used this method since april 1999 with good
results. I hope he will publish these results.
I rank this method as advanced.
Torsten Sillke,
Home |
FSP Mathematisierung |
Fakultät für Mathematik |
Universität Bielefeld
last changed 2009-01-04
